Today, it’s time to take our module to the next level. Lots of levels in fact! See, right now our module is full volume all the time. And well, music is more than notes and drum sounds—it needs dynamics! Fortissimo! pianissimo and every level in between. Of course, our General MIDI friends thought of this and, their solution has been staring at us the whole time! Here check out the MIDI note-on handler function:
void handleNoteOn( byte channel, byte midiNote, byte velocity ){
Velocity refers to the speed that you press a key on the keyboard. People often refer to this as “Touch Sensitivity,” but in most keyboards, this is a measure of key press speed, not the amount of pressure applied. There ARE keyboards that measure pressure, and that can be useful in something called “aftertouch” but we aren’t going there… yet…
Every time you press a key, a touch sensitive keyboard communicates both the note number and the velocity over MIDI. The MIDI library passes both of these values to the note on handler function. From there, it’s up to us to do something with it.
Level Scaling
Scaling the level of a channel should be pretty straight forward right? Just take the current level of the note and multiply it by the fraction of velocity / 127. This way high velocity notes will be louder proportionally to velocity. Right? Well, if it was that simple, this would be a boring article. So, not quite. There are a couple of gotchas here we need to talk about.
Operator Scaling
As you might suspect, the level setting controls the loudness of a channel. But level isn’t a channel setting. Level is an operator setting. And our patch definition has four different level settings per channel. So the question becomes, which level setting should we change? To figure that out, we need to review how an operator’s level affects the sound production.
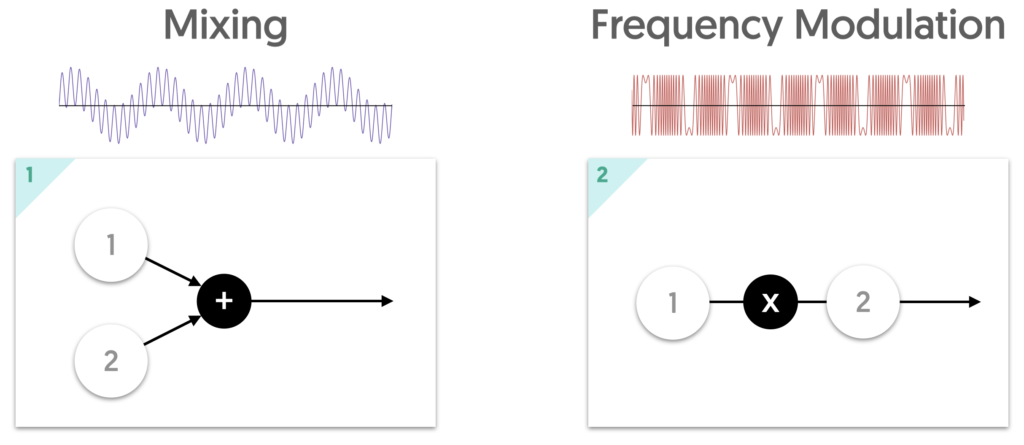
Mixing
Sticking with the two operator capability of a YM3812, there are only two ways to configure the “algorithm.” Mixing and Frequency Modulation. If we mix the two operators together, then BOTH operators contribute equally to the sound output. And, to scale that sound, we need to scale the level of BOTH operators.
Frequency Modulation
In frequency modulation mode, the two operators play very different roles—carrier and modulator. In this mode, only the carrier—operator 2—affects the level of the sound. The level of modulator—operator 1—affects the timbre of the output sound instead. So, we only want to scale the level of operator 2. If we scaled operator 1 as well, then the sound would become brighter the harder we press a key. This could be an interesting way to add after-touch, but again, not what we are trying to do today.
So, let’s put this all together:
- First check the algorithm to see if we are mixing or modulating
- If mixing, scale both operators
- If modulating, only scale the carrier operator (op2)
Calculating Level
Now that we know which numbers to combine, we need to figure out how these properties work. The YM3812 accepts a 6-bit value for the level property. That means it supports values from 0 through 63. On the other hand, the level value of our patch goes from 0 through 127. Take a look at article 6 if you need a refresher on why that is. Similarly, our velocity value also goes from 0 through 127 as well. To put these together, we need to scale level based on the percentage of velocity through 127.
patchLevel * velocity / 127
This formula results in values between 0 and 127, but we need those values to go from 0 to 63. So to fix that, we just need to divide the whole thing by 2 again. Or, better yet, divide by 256. (Yes I know that 127 x 2 is 254, but it actually doesn’t change the integer solutions and 256 is much easier to divide by):
patchLevel * velocity / 256
Let’s plot out some values based on this formula to better understand what’s going on. The table below shows patch levels (columns) and velocities (rows) from 0-127. I’ve also color coded the cells so things are easier to see:
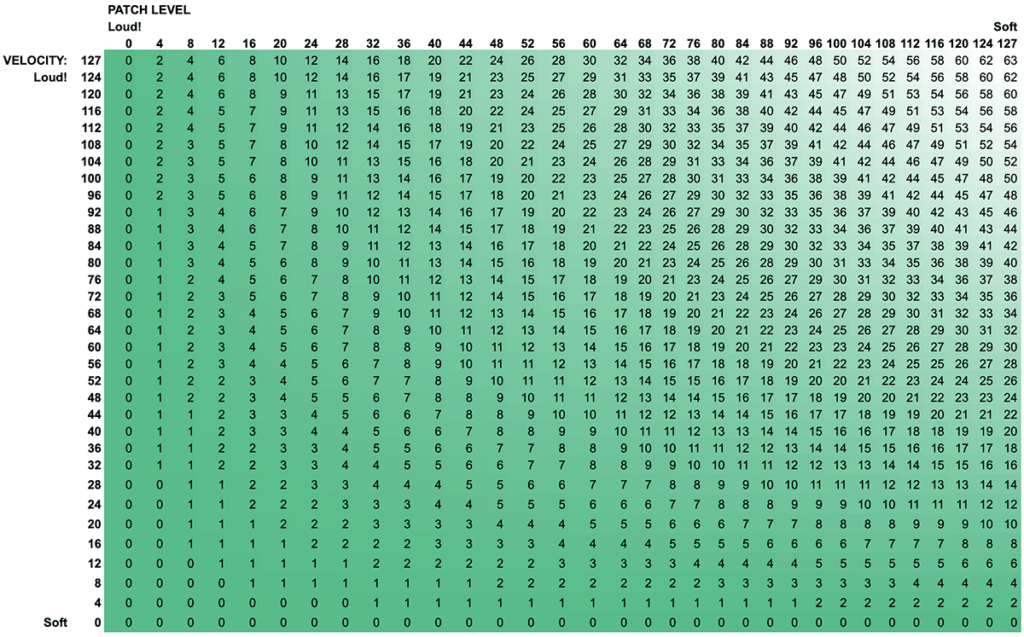
The color coding does a nice job here of showing how the highest values sit in the top right corner. And then those values decrease as you move left or down. This also brings to light our first “gotcha.” The value of Patch Level (for some reason) assumes that 0 is the loudest and 127 is the quietest. We need our values to radiate from the top left corner, instead of the top right. To do that, we can just invert the Patch Level:
(127-patchLevel) * velocity / 256
By subtracting patchLevel from the highest possible value (127), our table plot flips around. Let’s take a look:

Ok, now we are getting somewhere. The top left corner of the table appears to be going from loud to soft in all directions. Now for the second “gotcha.” The YM3812 also expects that zero is the loudest value. So now, we need to invert the entire table:
63 - ((127-patchLevel) * velocity / 256)
Just like before, we take the highest possible value (63) and subtract the entire formula. And now, plotting this out, you can see that the loudest values sit in the top left corner. As you move to a softer patch level (63) or a lower velocity (0) the formula gets closer to 63.
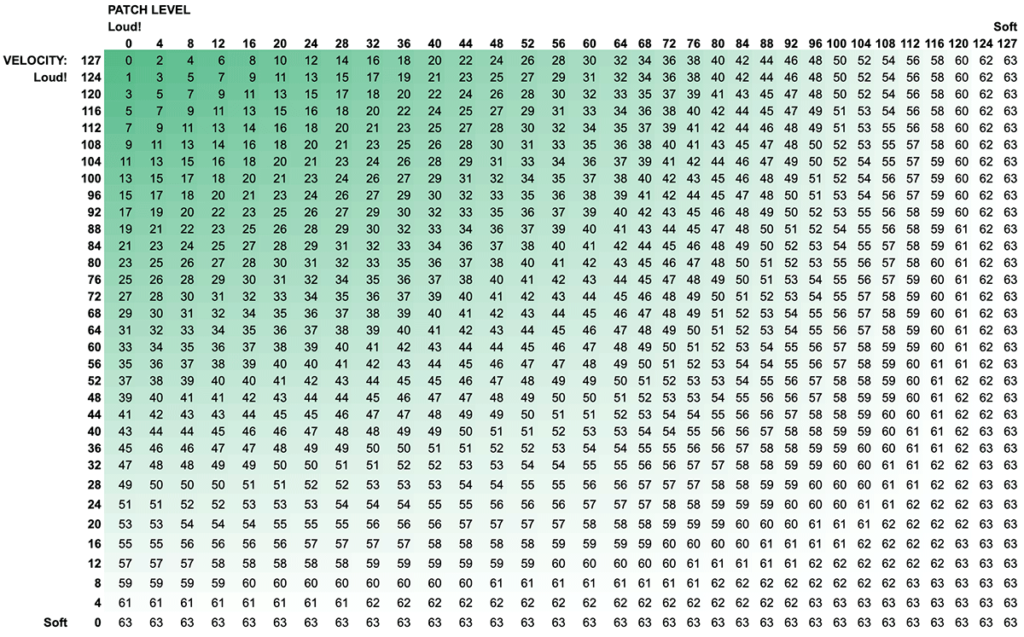
Beautiful. Now that we have our formula, let’s go write some code!
Code Updates!
For the most part, we only need to make a few tweaks from the last article. To keep this straightforward, let’s start at the noteHandler function and work our way inward.
void handleNoteOn( byte channel, byte midiNote, byte velocity ){
uint8_t ch = channel - 1;
uint8_t drumIndex;
if( DRUM_CHANNEL == channel ){
drumIndex = (midiNote - FIRST_DRUM_NOTE) % NUM_DRUMS;
PROC_YM3812.patchNoteOn( drum_patch_data[drumIndex], velocity );
} else {
PROC_YM3812.patchNoteOn( inst_patch_data[ch], midiNote, velocity );
}
}
The first change is pretty simple. We need to pass the velocity argument on to the patchNoteOn function of our YM3812 library. Of course for patchNoteOn to accommodate this new argument we have to update that too. So let’s do that next—starting with the function definition in the YM3812.h file:
void patchNoteOn( PatchArr &patch, uint8_t midiNote, uint8_t velocity );
void patchNoteOn( PatchArr &patch, uint8_t velocity ){
patchNoteOn( patch, patch[PATCH_NOTE_NUMBER], velocity);
}
Remember that there are two versions of the patchNoteOn function, and they both need to be updated. The second version simply calls the first, but now passes velocity along. Now let’s modify the patchNoteOn implementation. This code is in the YM3812.cpp file:
void YM3812::patchNoteOn( PatchArr &patch, uint8_t midiNote, uint8_t velocity ){
last_channel = chGetNext();
channel_states[ last_channel ].pPatch = &patch;
channel_states[ last_channel ].midi_note = midiNote;
channel_states[ last_channel ].velocity = velocity;
channel_states[ last_channel ].note_state = true;
channel_states[ last_channel ].state_changed = millis();
chPlayNote( last_channel, midiNote );
}
patchNoteOn chooses the next YM3812 channel and then keeps track of the note metadata. We are going to track velocity—just like the midiNote—by saving it into the channel_states array. The one new line of code in this function saves velocity into the channel_states entry for the current channel. This will make the information available later when we need to update the settings of the YM3812. Now, remember that channel_states is an array of YM_Channel data structures. So, to save velocity into it, we need to add a velocity property to the data structure:
struct YM_Channel{
PatchArr *pPatch = NULL;
uint8_t midi_note = 0;
uint8_t velocity = 127;
bool note_state = false;
unsigned long state_changed;
};
Logic Updates
After tracking the channel states, the patchNoteOn function calls chPlayNote which in turn calls chSendPatch before playing the note. And, chSendPatch configures the YM3812 for the instrument we want to play, and this is where we get to work our magic. For reference, here is the full function:
void YM3812::chSendPatch( byte ch, PatchArr &patch ){
uint8_t mem_offset, patch_offset;
uint8_t op_level;
//Channel Settings
sendData( 0xC0+ch, ((patch[PATCH_FEEDBACK]>>4)<<1) |
(patch[PATCH_ALGORITHM]>>6) );
for( uint8_t op = 0; op<2; op++ ){
mem_offset = op_map[channel_map[ch] + op*3];
patch_offset = PATCH_OP_SETTINGS * op;
if( (patch[PATCH_ALGORITHM] == 0) && (op==0) ){
op_level = patch[patch_offset + PATCH_LEVEL]>>1;
} else {
op_level = 63 - ((127 - patch[patch_offset + PATCH_LEVEL]) * channel_states[ ch ].velocity) >> 8);
}
sendData( 0x20+mem_offset, ((patch[patch_offset + PATCH_TREMOLO ]>>6)<<7) |
((patch[patch_offset + PATCH_VIBRATO ]>>6)<<6) |
((patch[patch_offset + PATCH_PERCUSSIVE_ENV ]>>6)<<5) |
((patch[patch_offset + PATCH_ENV_SCALING ]>>6)<<4) |
((patch[patch_offset + PATCH_FREQUENCY_MULT ]>>3)<<0) );
sendData( 0x40+mem_offset, ((patch[patch_offset + PATCH_LEVEL_SCALING ]>>5)<<6) |
op_level );
sendData( 0x60+mem_offset, ((patch[patch_offset + PATCH_ATTACK ]>>3)<<4) |
((patch[patch_offset + PATCH_DECAY ]>>3)<<0) );
sendData( 0x80+mem_offset, ((0xF-(patch[patch_offset + PATCH_SUSTAIN_LEVEL ]>>3))<<4) |
((patch[patch_offset + PATCH_RELEASE_RATE ]>>3)<<0) );
sendData( 0xE0+mem_offset, ((patch[patch_offset + PATCH_WAVEFORM ]>>5)<<0) );
}
}
Most of this function works exactly as it did before. But now, instead of using the operator’s level value in the patch data, we calculate it using some fancy math. And that math comes in the form of these 5 lines of code:
if( (patch[PATCH_ALGORITHM] == 0) && (op==0) ){
op_level = patch[patch_offset + PATCH_LEVEL]>>1;
} else {
op_level = 63 - ((127 - patch[patch_offset + PATCH_LEVEL]) * channel_states[ ch ].velocity) >> 8);
}
The first line of code decides whether or not to scale the level of the patch:
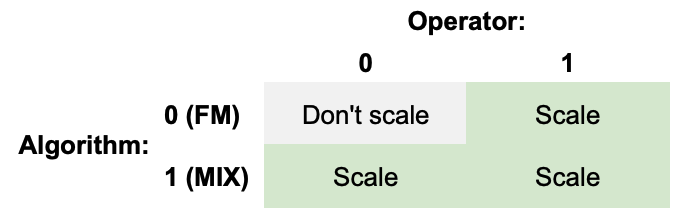
Thinking back to the algorithm we talked about earlier, there’s only one case where we don’t scale the level: when the algorithm is zero (FM mode) AND the operator is zero (the modulator operator). In this case, level controls timbre not volume, but in every other case, level affects the volume of the sound. Chips with more operators, require a more complex table, but this one is nice and simple.
The second line of code handles the “don’t scale” case by assigning the current patch’s level value to op_level. This line also right shifts the patch value by one so it falls into the 0 to 63 range. The fourth line handles the “do scale” case, and adjusts the patch’s level proportionally to velocity. While the code looks a little complicated, it really just derives from the formula we created earlier:
63 - ((127-patchLevel) * velocity / 256)
First let’s substitute patchLevel with the reference to the level value in the patch array:
63-((127-patch[patch_offset+PATCH_LEVEL]) * velocity) / 256)
Then, we swap velocity with the value from our channel_states array:
63-((127-patch[patch_offset+PATCH_LEVEL]) * channel_states[ ch ].velocity) / 256)
And finally, we use one more trick. Whenever you divide an integer by a power of 2, you can right shift instead to do it MUCH faster. Here, for example, we right shift by 8 bits to divide by 256. Because these are integers, you need to ensure that the numerator is larger than the denominator. This is why we multiply level and velocity before right shifting by 8—hence the parenthesis.
63-((127-patch[patch_offset+PATCH_LEVEL]) * channel_states[ ch ].velocity) >> 8)
And that’s how you derive that line of code. There’s one more small tweak to make in this function. We need to update the sendData command to use our newly calculated op_level value:
sendData( 0x40+mem_offset, ((patch[patch_offset + PATCH_LEVEL_SCALING ]>>5)<<6) |
op_level );
And that’s it! It’s…
Demo Time
In this first demo, let’s see how this SHOULD sound when only carrier operators are scaled:
Notice how the waveforms scale up and down with the note velocity, but otherwise doesn’t change? This works because in FM mode we don’t scale the modulator operator. Just for the heck of it, let’s see what happens when we scale everything including the modulator operator:
Notice here how the edges and corners of the waveforms become more pronounced as velocity increases. This is how that modulator operator affects the sound. Now, there may be times where it makes sense to have velocity change the quality of a note. Maybe a bass that gets more plucky the harder you play the note? That feels to me like a special case, but perhaps there is an opportunity to add velocity response as an operator property in the patch? Definitely open to feedback there.
Conclusion & Links
I don’t know about you, but I never thought scaling the level of a note would be so difficult. Still, this opens the door to some other cool features down the road like more granular panning—once we have multiple chips of course. As always you can find the code on GitHub. And if you run into any issues, feel free to drop a comment below. For the next article, I’m a bit torn between pitch bend and virtual 4-op voices. If you have a preference, let me know!
Till next time…





